报告人：邵井海教授

报告时间：5月20日（周 六）上午8:30—9:30

报告地点：统计与数据科学学院213

报告题目：Conditional McKean-Vlasov SDEs with jumps and Markovian regime-switching: wellposedness, propagation of chaos, averaging principle

报告摘要：The conditional McKean-Vlasov SDEs with jumps and Markovian regime-switching are investigated in this work. We propose a new metric on the cadlag path space to overcome the difficulty caused by the jumps in order to establish the strong wellposedness of conditional McKean-Vlasov SDEs using $L^2$-Wasserstein distance. Also, we establish the propagation of chaos for the associated mean-field interaction particle system with common noise and provide an explicit bound on the convergence rate. Furthermore, an averaging principle is established for   two time-scale conditional McKean-Vlasov equations, where much attention is paid to the convergence of the conditional distribution term.

报告人简介：邵井海，天津大学应用数学中心教授，博士生导师。2006年获得北京师范大学与法国第戎大学的理学博士学位。邵井海教授主要从事概率论遍历性理论、随机分析、随机微分方程方面的研究工作，在轨道空间和环空间上运输不等式、Monge-Kantorovich最优映射问题，以及带切换扩散过程长时间行为方面取得了重要成果。

报告人：翟建梁教授

报告时间：5月20日（周 六）上午9:30—10:30

报告地点：统计与数据科学学院213

报告题目：Irreducibility of SPDEs driven by pure jump noise

报告摘要：The irreducibility is fundamental for the study of ergodicity of stochastic dynamical systems. In the literature, there are very few results on the irreducibility of stochastic partial differential equations (SPDEs) and stochastic differential equations (SDEs) driven by pure jump noise. The existing methods on this topic are basically along the same lines as that for the Gaussian case. They heavily rely on the fact that the driving noises are additive type and more or less in the class of stable processes. The use of such methods to deal with the case of other types of additive pure jump noises appears to be unclear, let alone the case of multiplicative noises.

In this paper, we develop a new, effective method to obtain the irreducibility of SPDEs and SDEs driven by multiplicative pure jump noise. The conditions placed on the coefficients and the driving noise are very mild, and in some sense they are necessary and sufficient. This leads to not only significantly improving all of the results in the literature, but also to new irreducibility results of a much larger class of equations driven by pure jump noise with much weaker requirements than those treatable by the known methods. As a result, we are able to apply the main results to SPDEs with locally monotone coefficients, SPDEs/SDEs with singular coefficients, nonlinear Schrodinger equations, Euler equations etc. We emphasize that under our setting the driving noises could be compound Poisson processes, even allowed to be infinite dimensional. It is somehow surprising.

报告人简介：翟建梁，中国科学技术大学副教授，2010年获中国科学院数学与系统科学研究院博士。主要研究方向是Levy过程驱动的随机偏微分方程。已在 “J. Eur. Math. Soc.”、“J. Funct. Anal.”、“J. Math. Pures Appl.”等国际重要杂志发表论文三十余篇。

报告人：王冉教授

报告时间：5月20日（周 六）上午10:30—11:30

报告地点：统计与数据科学学院213

报告题目：Chung-type law of the iterated logarithm for the bifractional Brownian motion at the origin

报告摘要：

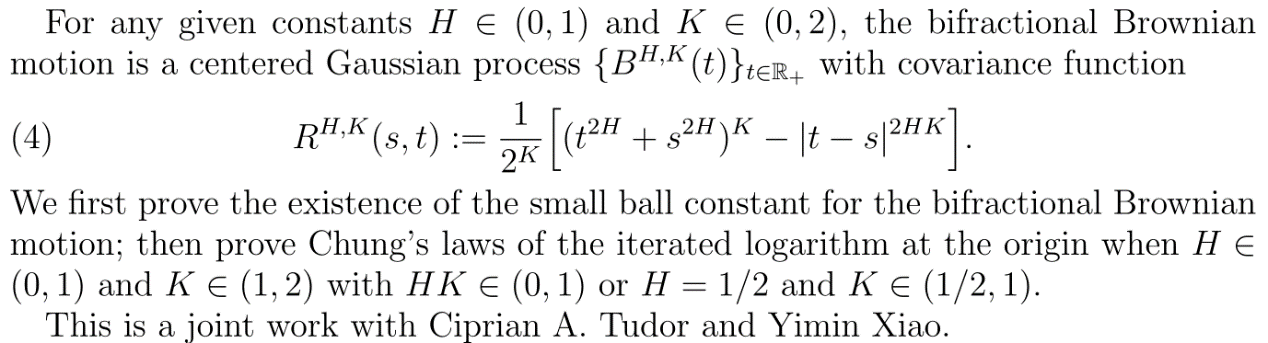
报告人简介：王冉，武汉大学数学与bwin必赢线路副教授。2012年博士毕业于武汉大学。 主要从事大偏差、泛函不等式和随机偏微分方程方面的研究工作。主持国家自然科学基金面上项目和青年项目各一项。